Stack 與 Queue 的相互實作

先看一下題目描述

225. Implement Stack using Queues

Implement a last-in-first-out (LIFO) stack using only two queues. The implemented stack should support all the functions of a normal stack (push, top, pop, and empty).

232. Implement Queue using Stacks

Implement a first in first out (FIFO) queue using only two stacks. The implemented queue should support all the functions of a normal queue (push, peek, pop, and empty).

這裡稍微補充說明一下，Stacks 和 Queues 是兩種方向不同的抽象資料結構（ADT）。如下圖所示，Stack 的特性是「FILO」，也就是說它提供同一個入口與出口，先被加入的元素會比較晚被取出。Queue 的特性是「FIFO」，也就是說它提供分別兩個入口與出口，從入口先被加入的元素會從出口比較早被取出。

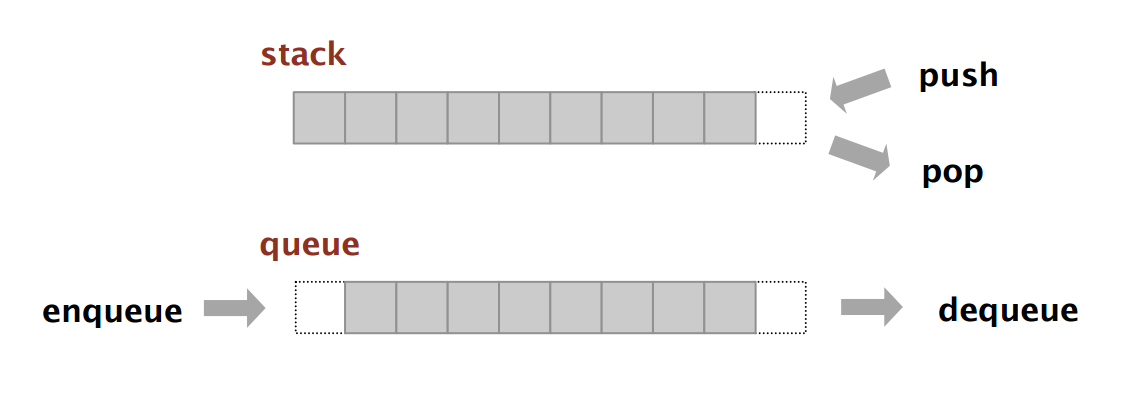
更多細節可以參考 Algorithms - Stacks and Queues 內文。

再搭配範例理解題目

class MyStack:
    def __init__(self):
    def push(self, x: int) -> None:
    def pop(self) -> int:
    def top(self) -> int:
    def empty(self) -> bool:

class MyQueue:
    def __init__(self):
    def push(self, x: int) -> None:
    def pop(self) -> int:
    def peek(self) -> int:
    def empty(self) -> bool:

# Your MyStack object will be instantiated and called as such:
obj = MyStack()
obj.push(x)
param_2 = obj.pop()
param_3 = obj.top()
param_4 = obj.empty()

# Your MyQueue object will be instantiated and called as such:
obj = MyQueue()
obj.push(x)
param_2 = obj.pop()
param_3 = obj.peek()
param_4 = obj.empty()

這個題目的形式類似於「填空題」，需要把題目中不同物件的細節補上。而這兩題想練習是「如何用 Stack 實作 Queue」以及「如何用 Queue 實作 Stack」。

開始實作

在理解完題目與條件之後，那我們下一步就開始「#初探直覺解」並且一起嘗試「#刻意優化」的過程：

225. Implement Stack using Queues

先來看 225. Implement Stack using Queues 這個題目，你需要知道這兩個結構擁有的特性以及限制：

• 目標：實現 Stack 中的「push」、「pop」、「top」和「empty」
• 來源：Queues

根據題目中有特別提到的注意事項：

You must use only standard operations of a queue, which means that only push to back, peek/pop from front, size and is empty operations are valid.

簡單來說，本題僅可使用 Queue 資料結構作為來源 ，而在 Queue 當中有兩種標準定義的方法：

• shift：取出最左邊（最早被加入）的元素
• push：新加入的元素會邊加入到最右邊

所以這個題目的限制是只能利用 Queue 的 peek 跟 push 方法實現 Stack 中的方法，初步的想法是在每次執行新增元素的時候，當將 Queue 中的元素倒序，可以達到「新加入的元素，將變成第一個被取出的元素」行為，也就是 FILO 的效果。

用 Python 實作一次

在 Python 中，我們會利用 [...] 代表 Queue，當中的 append(...) 用來 加入元素 、 [0]/pop(0) 用來 取出元素 。

class MyStack:

    def __init__(self):
        self.queue = []

    def push(self, x: int) -> None:
        self.queue.append(x)
        for _ in range(len(self.queue)-1):
            self.queue.append(self.queue[-1])
            self.queue = self.queue.remove(self.queue[-1])

    def pop(self) -> int:
        return self.queue.pop(0)
        

    def top(self) -> int:
        return self.queue[0]
        

    def empty(self) -> bool:
        return not self.queue

也可以用 JavaScript 復刻一次

在 JavaScript 中，我們會利用 [...] 代表 Queue，當中的 push(...) 用來 加入元素 、 [0]/shift() 用來 取出元素 。

var MyStack = function() {
   this.queue = []; 
};

MyStack.prototype.push = function(x) {
    this.queue.push(x);
    for(let i = 1; i < this.queue.length; i++){
        this.queue.push(this.queue.shift());
    }
};

MyStack.prototype.pop = function() {   
    return this.queue.shift();
};

MyStack.prototype.top = function() {
    return this.queue[0];
};

MyStack.prototype.empty = function() {
   return this.queue.length === 0; 
};

232. Implement Queue using Stacks

先來看 232. Implement Queue using Stacks 這個題目，你需要知道這兩個結構擁有的特性以及限制：

• 目標：實現 Queue 中的「push」、「pop」、「peek」和「empty」
• 來源：Stack

根據題目中有特別提到的注意事項：

You must use only standard operations of a stack, which means only push to top, peek/pop from top, size, and is empty operations are valid.

簡單來說，本題僅可使用 Stack 資料結構作為來源 ，而在 Stack 當中有兩種標準定義的方法：

• pop：取出最上邊（最新被加入）的元素
• push：新加入的元素會邊加入到最上方

所以這個題目的限制是只能利用 Stack 的 pop 跟 push 方法實現 Queue 中的方法，初步的想法是在每次執行新增元素的時候，當將 Stack 中的元素倒序，可以達到「新加入的元素，將變成最後一個被取出的元素」行為，也就是 FILO 的效果。

用 Python 實作一次

在 Python 中，我們會利用 [...] 代表 stack，當中的 append(...) 用來 加入元素 、 [-1]/pop() 用來 取出元素 。

class MyQueue:
      
    def __init__(self):
        self.stack = []

    def push(self, x):
        swap = []
        while self.stack:
            swap.append(self.stack.pop())
        swap.append(x)
        while swap:
            self.stack.append(swap.pop())

    def pop(self) -> int:
        return self.stack.pop()

    def peek(self) -> int:
        return self.stack[-1]

    def empty(self) -> bool:
        return not self.stack

也可以用 JavaScript 復刻一次

在 JavaScript 中，我們會利用 [...] 代表 Queue，當中的 push(...) 用來 加入元素 、 [this.stack.length-1]/pop() 用來 取出元素 。

    var MyQueue = function() {
        this.stack = [];
    };

    MyQueue.prototype.push = function(x) {
        swap = []
        while(this.stack.length > 0)
            swap.push(this.stack.pop());
        swap.push(x)
        while(swap.length > 0)
            this.stack.push(swap.pop()); 
    };

    MyQueue.prototype.pop = function() {
        return this.stack.pop();
    };

    MyQueue.prototype.peek = function() {
        return this.stack[this.stack.length-1];
    };

    MyQueue.prototype.empty = function() {
        return this.stack.length === 0; 
    };

反思沉澱

這個題目是關於 Stack 和 Queue 的經典實作題，他們是兩種方向不同的抽象資料結構（ADT）。也就是說，我們會定義一個 Stack 或 Queue 需要有哪些方法與特性，但我們不會特別限制實際上如何實現，因此常見的方法可以利用陣列、陣列串鏈來實作。而這個題目比較特別的是，如何用 Stack 與 Queue 兩個結構相互實作。因此，必須要了解這兩個結構的特性與方法並且能夠進一步運用，才能更有效地完成該題目。

嗨，大家好！我是維元，一名擅長網站開發與資料科學的雙棲工程師，斜槓於程式社群【JSDC】核心成員及【資料科學家的工作日常】粉專經營。目前在 ALPHACamp 擔任資料工程師，同時也在中華電信、工研院與多所學校等單位持續開課。擁有多次大型技術會議講者與競賽獲獎經驗，持續在不同的平台發表對 #資料科學、 #網頁開發 或 #軟體職涯 相關的分享，邀請你加入 訂閱 接收最新資訊。